Why GPT canot compare 9.11 and 9.9
Cuz this is a virus meme on Chinese social media, this post is first wirtten in Chinese.
最近有大量的群聊在讨论为什么GPT无法正确地比较9.11和9.9



可以看到无论是微软的Copilot,还是GPT4o,或者调用GPT API的外部网站,都无法正确地比较9.11和9.9的大小,最好玩的是即使程序已经明白地输出9.9 > 9.12, GPT仍然坚信自己的“常识”。
其实一句话就可以讲清楚原理:
Openai使用的分词模型会把 9.9 分词为 ‘9’ 和 ‘.’ 和 ‘9’, 而把 9.12 分词为 ‘9’ 和 ‘.’ 和 ‘12’,由于 Transformer 不像 RNN 一样有天然有文字的前后顺序关系,是一种位置不敏感 (position-incencitive) 的架构,因此处理有前后顺序的词没那么容易,所以就很难比较了。
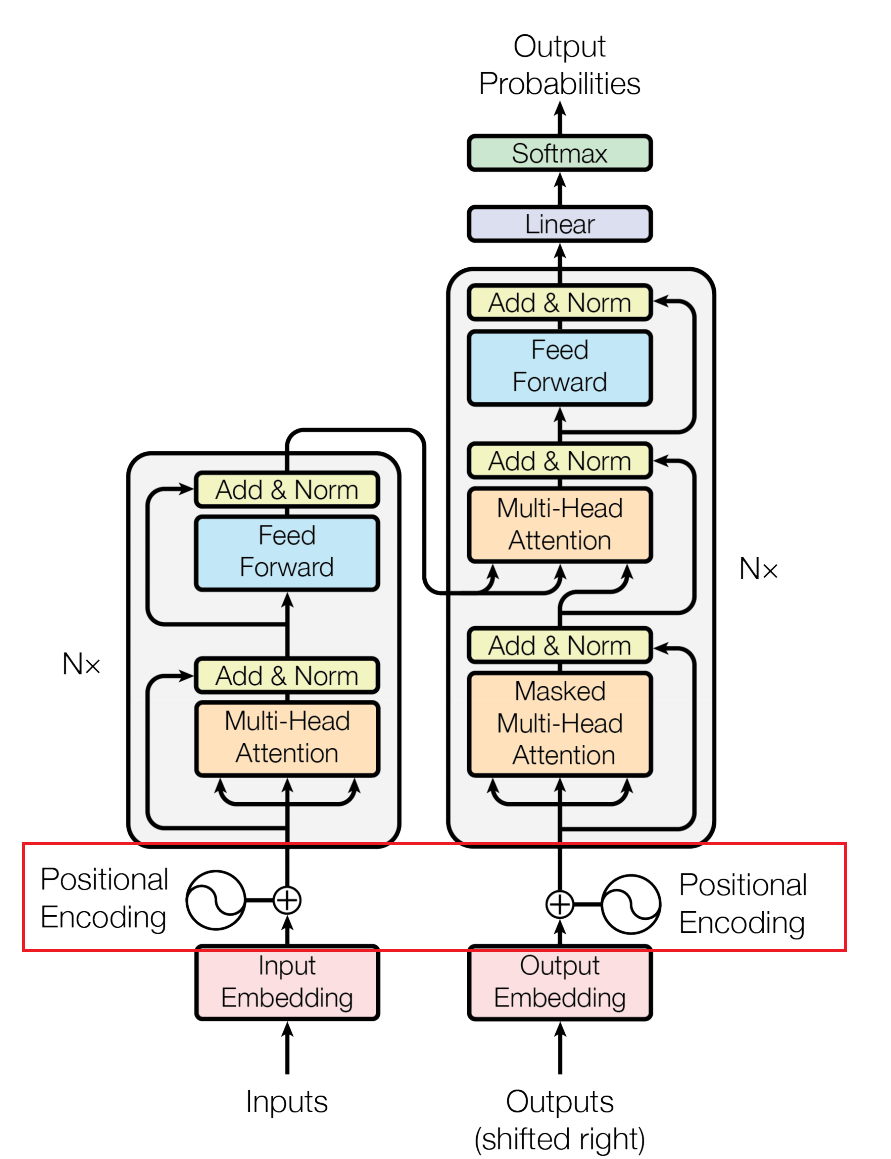
但其实我们可以想远一点, Transformer 也是有使用 Postional Encoding 的,为什么还是没能解决这个问题呢?
有一项在21年进行的研究以实验的方式证明了各种编码方式在小数位数增加时能力都在显著下降:Investigating the Limitations of Transformers with Simple Arithmetic Tasks, R. N, etl. University of Waterloo

文章指出:
Models tend to perform better with explicit position tokens that clarify the significance of digits within numbers. However, standard decimal representations can cause confusion, particularly when numbers are not systematically broken down into consistent and recognizable tokens. This issue can lead models to fail at tasks involving large numbers due to the difficulty in accurately determining digit significance from inconsistent token embeddings.
也就是使用严格绝对位置结果会更好,考虑到Transformer使用的是相对位置编码:
不难理解 pos 与 pos+1 对 Transformer 来说区分的难度还是太大了。
文章还提出了一种绝对的数字编码方式,使用这种方式会提高 Transformer 对大量数学任务的处理能力。
这个问题其实和 MLP 做奇数偶数判别器一样,可以让我们深入地思考为什么看似强大的模型还存在着诸多能力的缺陷,也更让我们对模型设计这门学问感到崇敬。
English Version
Recently, there has been a lot of discussion in group chats about why GPT cannot correctly compare 9.11 and 9.9. This quirk reveals deeper complexities about how machines understand the world.



As you can see, neither Microsoft’s Copilot, GPT-4, nor external websites calling the GPT API can correctly compare the sizes of 9.11 and 9.9. The most amusing part is that even when the program explicitly outputs 9.9 > 9.12, GPT still insists on its “common sense.”
The principle can be explained in one sentence:
OpenAI’s tokenization model splits 9.9 into ‘9’, ‘.’, and ‘9’, while it splits 9.12 into ‘9’, ‘.’, and ‘12’. Tokenization is the process of breaking down text into smaller parts, like words or numbers. Because the Transformer, unlike RNN, does not have a natural sense of sequence in the text and is a position-insensitive architecture, it is not easy to handle sequential words, making it difficult to compare them correctly.
However, we can think further. Transformers also use Positional Encoding, so why hasn’t this issue been resolved?

A study conducted in 2021 experimentally proved that the capabilities of various encoding methods significantly decline as the number of decimal places increases: Investigating the Limitations of Transformers with Simple Arithmetic Tasks, R. N., et al., University of Waterloo.

The article points out:
Models tend to perform better with explicit position tokens that clarify the significance of digits within numbers. However, standard decimal representations can cause confusion, particularly when numbers are not systematically broken down into consistent and recognizable tokens. This issue can lead models to fail at tasks involving large numbers due to the difficulty in accurately determining digit significance from inconsistent token embeddings.
In other words, using strict absolute positioning yields better results. Considering that the Transformer uses relative positional encoding:
It’s not hard to understand that distinguishing between pos and pos+1 is still too challenging for the Transformer.
The article also proposes an absolute number encoding method, which improves the Transformer’s ability to handle many mathematical tasks.
This issue is similar to using MLP as an odd-even discriminator. It allows us to delve deeply into why seemingly powerful models still have many capability shortcomings and further appreciate the complexity of model design.