Qwen QwQ for Solving Mathematical Problems: A Comprehensive Guide

In the rapidly evolving landscape of artificial intelligence, language models have transcended traditional boundaries, enabling applications that were once deemed impossible. Among these, QwQ https://qwenlm.github.io/blog/qwq-32b-preview/ stands out as a formidable tool for tackling complex mathematical problems. In this blog post, we’ll delve into how to effectively utilize QwQ by walking through a detailed example codebase. Whether you’re a data scientist, AI enthusiast, or a Kaggle competitor, this guide will equip you with the knowledge to harness QwQ’s capabilities for mathematical problem-solving.

This guide is to solve this kaggle competition. The nodebook is open-sourced here.

Introduction to QwQ

QwQ is a cutting-edge CoT (Chain-of-Thought) language model designed to understand and generate human-like text. Leveraging transformer architectures, QwQ excels in various natural language processing tasks, including text generation, translation, summarization, and notably, mathematical problem-solving. Its ability to comprehend complex instructions and perform step-by-step reasoning makes it an invaluable tool for tackling intricate mathematical challenges.

In this guide, we’ll explore how to deploy QwQ to solve mathematical problems by integrating it with Python code execution and serving predictions through an inference server. This comprehensive approach ensures not only accurate answers but also validates the reasoning process behind them.

Understanding the Code Structure

The provided code is a comprehensive pipeline designed to:

1. Load and Configure the QwQ Model:

   • Initialize the language model with specific parameters.
   • Set up the tokenizer for processing inputs and outputs.

2. Generate and Process Prompts:

   • Use engineered prompts to guide the model’s reasoning process.
   • Extract Python code from the model’s responses for execution.

3. Execute Python Code:

   • Run the extracted code in a secure, isolated environment.
   • Capture outputs to verify and refine the model’s answers.

4. Aggregate and Select the Final Answer:

   • Collect answers from multiple reasoning paths.
   • Use statistical methods to determine the most reliable answer.

Let’s break down each component in detail.

Loading and Configuring the QwQ Model

Model Path Configuration

The first step involves specifying the path to the QwQ model. This path points to the location where the model’s weights and configurations are stored.

1

llm_model_pth = 'Your_Path/qwen2.5/transformers/qwq-32b-preview-awq/1'

Initializing the Language Model

Using the vllm library, we initialize the QwQ model with specific parameters tailored for our use case:

1
2
3
4
5
6
7
8
9
10

from vllm import LLM, SamplingParams

llm = LLM(
    llm_model_pth,
    max_model_len=32768,              # Extends context length for long inputs
    trust_remote_code=True,           # Allows execution of remote code (use with caution)
    tensor_parallel_size=4,            # Utilizes 4 GPUs for parallel processing
    gpu_memory_utilization=0.96,       # Reserves 4% GPU memory for overhead
)
tokenizer = llm.get_tokenizer()

Key Parameters:

• max_model_len: Sets an extensive context window, allowing the model to process and generate long sequences.
• trust_remote_code: Enables the model to execute code from remote repositories. Caution: This can pose security risks if the source is untrusted.
• tensor_parallel_size: Distributes the model across multiple GPUs, enhancing performance for large-scale models.
• gpu_memory_utilization: Manages GPU memory allocation to prevent overuse.

Hyper Params

1
2
3
4
5
6
7

sampling_params = SamplingParams(
    temperature=1.0,
    min_p=0.01,
    skip_special_tokens=True,
    max_tokens=32768,

)

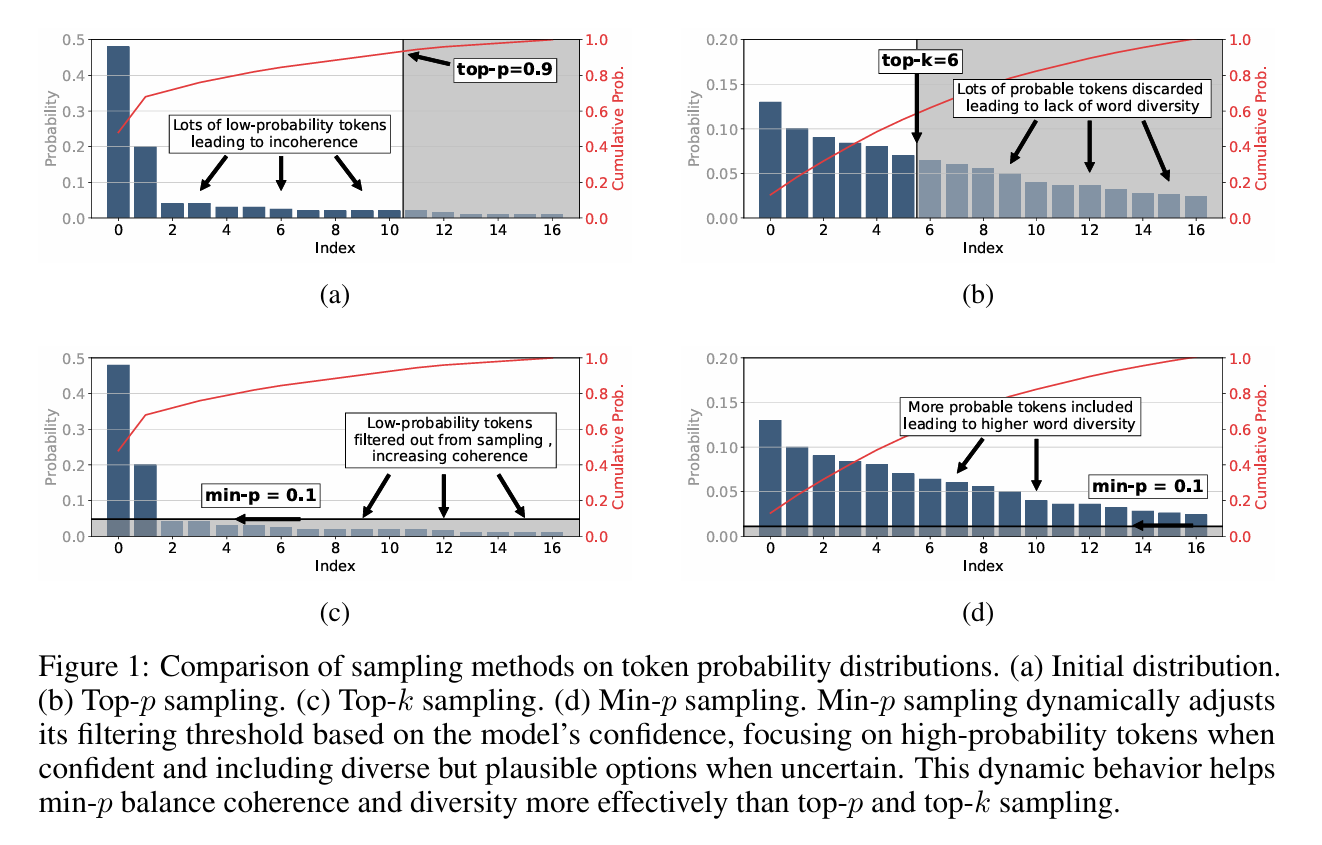
Here, min p is from this paper.

“min p” is a sampling technique used during text generation to select the next word (or token) in a sequence. It aims to strike a balance between the creativity and coherence of the generated text by setting a minimum probability threshold relative to the most probable word. Let’s delve into the details:

1. Core Concepts:

Probability Distribution: When an LLM generates text, it assigns a probability to each word in its vocabulary, representing the likelihood of that word being the next in the sequence. These probabilities form a probability distribution.
Most Probable Word (Pmax): Within this distribution, the word with the highest probability is termed the “most probable word,” and its probability is denoted as Pmax.
Relative Probability (Pbase): The relative probability of other words is their probability divided by Pmax: Pbase = P(word) / Pmax. This gives you a sense of how likely a word is compared to the most likely option.
Scaled Probability (Pscaled): The min p sampling method uses a scaled probability as a selection criterion: Pscaled = min p * Pmax. Only words with a probability greater than or equal to Pscaled are considered for selection.

2. How min p Works:

The fundamental idea behind min p is to only consider words whose probability is at least a certain proportion of the “most probable word’s” probability. This proportion is defined by the min p value.

Example: Suppose Pmax is 50%. If min p is set to 0.1, then Pscaled = 0.1 * 50% = 5%. This means only words with a probability of 5% or higher will be considered during the sampling process.

3. The Relationship Between min p and Selected Word Probabilities:

Smaller min p Values: A smaller min p value means a smaller Pscaled, allowing more words with lower probabilities to be included in the selection pool. This leads to more diverse and creative text generation but may also reduce the text’s coherence. The model is willing to explore less likely options.
Larger min p Values: Conversely, a larger min p value results in a larger Pscaled, meaning only words with probabilities very close to Pmax are considered. This leads to more conservative and coherent text generation but may also make the output monotonous and repetitive. The model sticks closer to the most probable choices.

4. Visual Representation:

Imagine a graph where the x-axis represents word probabilities and the y-axis represents the rank of words (sorted by probability from highest to lowest). Different curves on the graph could represent different min p values. The area under each curve would then represent the range of probabilities of words that would be selected. A lower min p value would have a larger area under the curve, signifying a wider range of probabilities being considered.

Prompt Engineering for Mathematical Reasoning

Effective prompting is crucial for guiding the model’s reasoning process. The code employs a set of carefully crafted prompts designed to elicit step-by-step reasoning and structured answers.

1
2
3
4
5
6
7

thoughts = [
    'Please use chained reasoning to put the answer in \\boxed{}.',
    'Please reflect and verify while reasoning and put the answer in \\boxed{}.',
    'Solve the following problem using concise and clear reasoning by placing the answer in \\boxed{}.',
    'You are a helpful and reflective maths assistant, please reason step by step to put the answer in \\boxed{}.',
    'You are the smartest maths expert in the world, please spike this question and put the answer in \\boxed{}.'
]

Purpose of the Prompts:

• Structured Reasoning: Directs the model to perform step-by-step reasoning, enhancing the transparency and reliability of its answers.
• Answer Formatting: Instructs the model to encapsulate the final answer within a LaTeX \boxed{} environment, facilitating easy extraction.

Generating the Next Prompt

To introduce variability and prevent the model from falling into repetitive patterns, the make_next_prompt function cycles through the predefined prompts:

1
2
3
4

def make_next_prompt(text, round_idx):
    default_prompt = thoughts[(round_idx + 1) % len(thoughts)]
    default_python_code = f"print('{default_prompt}')"
    return default_python_code

Extracting and Executing Python Code

One of the innovative aspects of this approach is extracting Python code from the model’s output to verify and compute answers programmatically.

Extracting Python Code

The model is expected to embed Python code snippets within markdown code blocks. The following functions parse the model’s response to extract these code snippets:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

import re

def extract_python_code(text):
    pattern = r'```python\s*(.*?)\s*```'
    matches = re.findall(pattern, text, re.DOTALL)
    if matches:
        ans = "\n\n".join(matches)
        return ans
    return ""

def extract_python_code_list(text):
    pattern = r'```python\s*(.*?)\s*```'
    ans = []
    matches = re.findall(pattern, text, re.DOTALL)
    for m in matches:
        ans.append(m)
    return ans

Executing the Extracted Code

To safely execute the extracted Python code, the PythonREPL class is implemented:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41

import os
import tempfile
import subprocess

class PythonREPL:
    def __init__(self, timeout=8):
        self.timeout = timeout

    def __call__(self, query):
        with tempfile.TemporaryDirectory() as temp_dir:
            temp_file_path = os.path.join(temp_dir, "tmp.py")
            with open(temp_file_path, "w", encoding="utf-8") as f:
                f.write(query)
            
            try:
                result = subprocess.run(
                    ["python3", temp_file_path],
                    capture_output=True,
                    check=False,
                    text=True,
                    timeout=self.timeout,
                )
            except subprocess.TimeoutExpired:
                return False, f"Execution timed out after {self.timeout} seconds."

            stdout = result.stdout.strip()
            stderr = result.stderr.strip()

            if result.returncode == 0:
                return True, stdout
            else:
                # Clean the error message by removing the temporary file path
                error_lines = stderr.split("\n")
                cleaned_errors = []
                for line in error_lines:
                    if temp_file_path in line:
                        line = line.replace(temp_file_path, "<temporary_file>")
                    cleaned_errors.append(line)
                cleaned_error_msg = "\n".join(cleaned_errors)
                combined_output = f"{stdout}\n{cleaned_error_msg}" if stdout else cleaned_error_msg
                return False, combined_output

Aggregating and Selecting the Final Answer

After extracting and executing Python code, the system aggregates the results to determine the most reliable answer.

Extracting Boxed Texts

The model’s final answers are expected to be enclosed within \boxed{}. The following function extracts these numerical values:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

def extract_boxed_texts(text):
    pattern = r'\\boxed{(.*?)}'
    matches = re.findall(pattern, text)
    if not matches:
        return []
    ans = []
    for content in matches:
        if content.isdigit():
            num = int(content)
        else:
            nums = re.findall(r'\d+', content)
            if not nums:
                continue
            num = int(nums[-1])
        ans.append(num % 1000)
    return ans

Selecting the Most Reliable Answer

Given multiple potential answers from various reasoning paths, the select_answer function employs a consensus mechanism:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

from collections import Counter

def select_answer(answers):
    valid_answers = []
    for answer in answers:
        try:
            if int(answer) == float(answer):
                if 1 < int(answer) < 999 and int(answer) % 100 > 0:
                    valid_answers.append(int(answer))
        except:
            pass
    if not valid_answers:
        return 49  # Default fallback answer
    _, answer = sorted([(v, k) for k, v in Counter(valid_answers).items()], reverse=True)[0]
    return answer % 1000

Handling Predictions and Responses

Combine all above together.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58

from collections import Counter, defaultdict

# Global variables for tracking performance
g_score = 0
g_count = 0
prompt_score = Counter()
answer_contributions = defaultdict(list)

def predict_for_question(question: str) -> int:
    global g_score
    global g_count
    global prompt_score
    global answer_contributions
    
    # Append directive for modulo operation
    question += "\nIf the final answer is a number larger than 1000, take modulo 1000. "
    
    # Check for cutoff time or environment variable
    if time.time() > cutoff_time or not os.getenv('KAGGLE_IS_COMPETITION_RERUN'):
        return 210  # Default answer if conditions are not met
    
    print(question)
    
    # Initialize multiple message sequences with different prompts
    list_of_messages = [
        [
            {"role": "system", "content": thoughts[k]},
            {"role": "user", "content": question}
        ] for k in range(5)
    ]

    all_extracted_answers = []
    list_of_idx = list(range(len(list_of_messages)))
    max_round = 1  # Can be increased for iterative refinement
    
    for round_idx in range(max_round):
        print(f"round {round_idx + 1}")
        list_of_messages = batch_message_generate(list_of_messages)
        extracted_python_answer = batch_message_list_execute_and_get_answer(list_of_messages, round_idx)
        list_of_messages, extracted_answers, list_of_idx  = batch_message_filter(list_of_messages, list_of_idx)
        all_extracted_answers.extend(extracted_python_answer)
        all_extracted_answers.extend(extracted_answers)
        print("extracted boxed answers:", extracted_answers)
        print("extracted python answers:", extracted_python_answer)
        print("all extracted answers:", all_extracted_answers)
        if not list_of_messages:
            break

    answer = select_answer(all_extracted_answers)
    print("answer:", answer)
    correct_answer = get_correct_answer(question)
    print("correct answer:", correct_answer)
    g_count += 1
    if str(answer) == str(correct_answer):
        g_score += 1
    print(f"score: {g_score}/{g_count}")
    print("\n\n")
    return answer

Pros and Cons of This Approach

Pros

1. Comprehensive Pipeline: The code covers the entire workflow from model loading to serving predictions, providing an end-to-end solution.
2. Structured Reasoning: Using engineered prompts and executing Python code ensures that the model’s reasoning is transparent and verifiable.
3. Scalability: Leveraging tensor parallelism and GPU optimization allows handling large models and high-throughput predictions.
4. Automated Verification: Executing extracted code provides a mechanism to validate and refine the model’s answers programmatically.
5. Integration with Kaggle: Tailored for Kaggle competitions, the code seamlessly fits into competitive environments, enhancing its practical utility.

Cons

1. Security Risks: Executing code extracted from model outputs poses significant security threats, even within temporary directories and with timeouts.
2. Dependence on Formatting: The extraction functions rely heavily on the model’s adherence to specific output formats (e.g., \boxed{}), which may not always hold. (In fact, in my test cases there’s high potential it wont follow the format instruction.)

Conclusion

Harnessing the capabilities of QwQ for solving mathematical problems offers a powerful blend of natural language understanding and computational verification. By integrating structured prompting, Python code execution, and an efficient inference server, this approach ensures both accuracy and reliability in the answers generated.