From RL to RLHF

Source:

Aligning language models to follow instructions https://openai.com/index/instruction-following/
A Comprehensive Survey of LLM Alignment Techniques: RLHF, RLAIF, PPO, DPO and More https://arxiv.org/pdf/2407.16216
Learning from human preferences https://openai.com/index/learning-from-human-preferences/
Deep reinforcement learning from human preferences https://arxiv.org/abs/1706.03741
Detailed Formulas https://zhuanlan.zhihu.com/p/7461863937
DeepSpeed Chat https://github.com/microsoft/DeepSpeedExamples/blob/master/applications/DeepSpeed-Chat/README.md

Note: This blog is a small part of these sources, recommend read them all.

TL; DR

This paper categorizes techniques for aligning large language models (LLMs) into four main themes with subtopics:

Reward Models
- Explicit vs. Implicit Models
- Pointwise vs. Pairwise Preference Models
- Response-Level vs. Token-Level Rewards
- Negative Preference Optimization
Feedback
- Preference Feedback vs. Binary Feedback
- Pairwise vs. Listwise Feedback
- Human Feedback vs. AI Feedback
Reinforcement Learning (RL)
- Reference-Based RL vs. Reference-Free RL
- Length-Controlled RL
- Online vs. Offline RL Strategies
- Subfields of RL Techniques
Optimization
- Iterative (Online) vs. Non-Iterative (Offline) Preference Optimization
- Separate vs. Combined SFT (Supervised Fine-Tuning) and Alignment

Key Techniques:

RLHF (Reinforcement Learning from Human Feedback): Aligns LLMs with user intent using human-labeled rewards and policies.
RLAIF (Reinforcement Learning from AI Feedback): Utilizes AI-generated feedback to enhance alignment.
Direct Preference Optimization (DPO): Aligns LLMs by directly optimizing preferences rather than modeling reward signals.
Iterative/Online Methods: Enables dynamic fine-tuning for out-of-distribution tasks.

Emerging Trends:

Token-Level Optimization for granular alignment.
Binary Feedback Systems for scalability.
Nash Learning Approaches to address inconsistencies in pairwise preferences.
Combined SFT and Alignment to improve efficiency while mitigating catastrophic forgetting.

Let’s start from RL

Skipped all inference here

TL; DR: In RL, the Actor-Critic framework combines policy-based and value-based methods, where the actor updates the policy by choosing actions, and the critic evaluates the actions by estimating the value function, helping to reduce variance and improve learning efficiency.

Key Concepts and Notations

State ( $s_t$ ): The environment’s state at time step t.
Action ( $a_t$ ): The action taken by the agent at time step t.
Policy ( $\pi_\theta(a_t | s_t)$ ): A parameterized probability distribution over actions a_t given state s_t.
Reward ( $r_t$ ): The scalar feedback received after taking action a_t in state s_t.
Return ( $V_t$ ): The cumulative reward starting from time step t:
$V_t = \sum_{k=0}^\infty \gamma^k r_{t+k+1}$
where $\gamma \in [0, 1)$ is the discount factor.

Objective Function

The goal is to maximize the expected cumulative reward:

J(\theta) = \mathbb{E}_{\pi_\theta} \left[ V_t \right] = \mathbb{E}_{\pi_\theta} \left[ \sum_{t=0}^\infty r_t \right]

Using the policy gradient theorem, the gradient of $J(\theta)$ is:

\nabla_\theta J(\theta) = \mathbb{E}_{\tau \sim \pi_\theta} \left[ \sum_{t=0}^\infty \nabla_\theta \log \pi_\theta(a_t | s_t) V_t \right]

Advantage Function

To reduce variance, the advantage function $A_t$ is often used instead of $V_t$ :

A_t = Q^\pi(s_t, a_t) - V^\pi(s_t)

Definitions:

State-value function ( $V^\pi(s_t)$ ):

V^\pi(s_t) = \mathbb{E}_{a_t \sim \pi_\theta} \left[ V_t \mid s_t \right]

Action-value function ( $Q^\pi(s_t, a_t)$ ):

Q^\pi(s_t, a_t) = \mathbb{E}_{\tau \sim \pi_\theta} \left[ V_t \mid s_t, a_t \right]

Using the advantage function, the gradient becomes:

\nabla_\theta J(\theta) = \mathbb{E}_{\tau \sim \pi_\theta} \left[ \sum_{t=0}^\infty \nabla_\theta \log \pi_\theta(a_t | s_t) A^\pi(s_t, a_t) \right]

Actor-Critic Framework

The Actor-Critic method combines policy-based and value-based approaches:

Actor: Represents the policy $\pi_\theta(a_t | s_t)$ .
Critic: Estimates the value function $V^\pi(s_t)$ or $Q^\pi(s_t, a_t)$ .

The critic minimizes the Temporal Difference (TD) error:

\delta_t = r_t + \gamma V^\pi(s_{t+1}) - V^\pi(s_t)

The actor updates the policy using:

\nabla_\theta J(\theta) = \mathbb{E}_{\tau \sim \pi_\theta} \left[ \nabla_\theta \log \pi_\theta(a_t | s_t) \delta_t \right]

Generalized Advantage Estimation (GAE)

The Generalized Advantage Estimation (GAE) smooths the advantage function for better bias-variance trade-off:

A_t^\text{GAE} = \sum_{k=0}^\infty (\gamma \lambda)^k \delta_{t+k}

where:

$\lambda \in [0, 1]$ : A smoothing parameter.
$\delta_t = r_t + \gamma V^\pi(s_{t+1}) - V^\pi(s_t)$ .

Algorithm Summary (Vanilla Policy Gradient)

Sample Trajectories: Collect N trajectories $\{\tau_i\}_{i=1}^N$ using the current policy $\pi_\theta$ .
Estimate Rewards: Compute $V_t$ or $A_t$ for each time step.
Compute Policy Gradient:

\nabla_\theta J(\theta) = \frac{1}{N} \sum_{i=1}^N \sum_{t=0}^{T_i} \nabla_\theta \log \pi_\theta(a_t^i | s_t^i) A_t^i

Update Policy:

\theta \gets \theta + \alpha \nabla_\theta J(\theta)

where $\alpha$ is the learning rate.

Comparison: Policy-based vs. Value-based RL

Aspect	Policy-based RL	Value-based RL
Core Objective	Directly learns the policy $\pi_\theta(a	s)$.
Strategy	Optimizes the policy to maximize cumulative rewards.	Derives the policy indirectly by maximizing the value function.
Action Space	Handles both continuous and discrete action spaces well.	Primarily suited for discrete action spaces.
Exploration	Naturally supports stochastic exploration.	Requires $\epsilon$ -greedy or similar exploration strategies.
Convergence	More stable due to directly optimizing the objective.	Can oscillate as policy is derived from value updates.
Sample Efficiency	Less efficient; requires many samples for policy updates.	More sample efficient due to value function updates.
Common Methods	REINFORCE, PPO, TRPO, Actor-Critic.	Q-Learning, DQN, SARSA.

From Actor-Critic to LLM RLHF

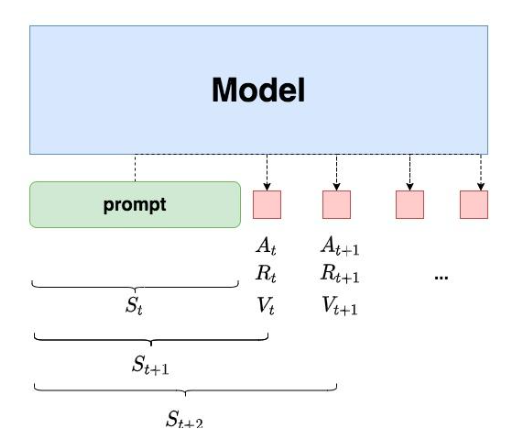
So, how do we map this RL process to NLP tasks? In other words, what do the agent, environment, state, action, etc., represent in the context of NLP tasks?

Recall the purpose of applying reinforcement learning (RLHF) to NLP tasks: we want to provide a model with a prompt, and the model should generate responses that align with human preferences. Now, recall the reasoning process of the GPT model: at each step, the model generates a single token, meaning tokens are produced one after another, with the current token relying on the previous token.

With these points in mind, we can now better interpret the diagram above:

We first provide the model with a prompt and expect it to generate a response that aligns with human preferences.
At time step $t_1$ , the model generates a token $a_1$ based on the prompt and previous context, and this token corresponds to the action in reinforcement learning. Hence, it’s easy to understand that, in the NLP context, the action space of the RL task corresponds to the vocabulary.
At time step $t_2$ , the model generates token $a_2$ , and the immediate reward $r_2$ is obtained, with the total return $V_2$ being the sum of all future rewards (recall that $V_t$ encapsulates both “immediate rewards” and “future rewards”).
This reward can be understood as a “measure of human preference.” At this point, the model’s state transitions from $s_1$ to $s_2$ , i.e., from the “previous context” to the “previous context + new token.”
In the NLP context, the agent is the language model itself, and the environment corresponds to the text it generates.

Note: $R_t$ (the immediate reward) and $V_t$ (the total return) are not directly generated by the language model. They are instead generated by two other models, which will be explained in detail later.

RLHF-PPO

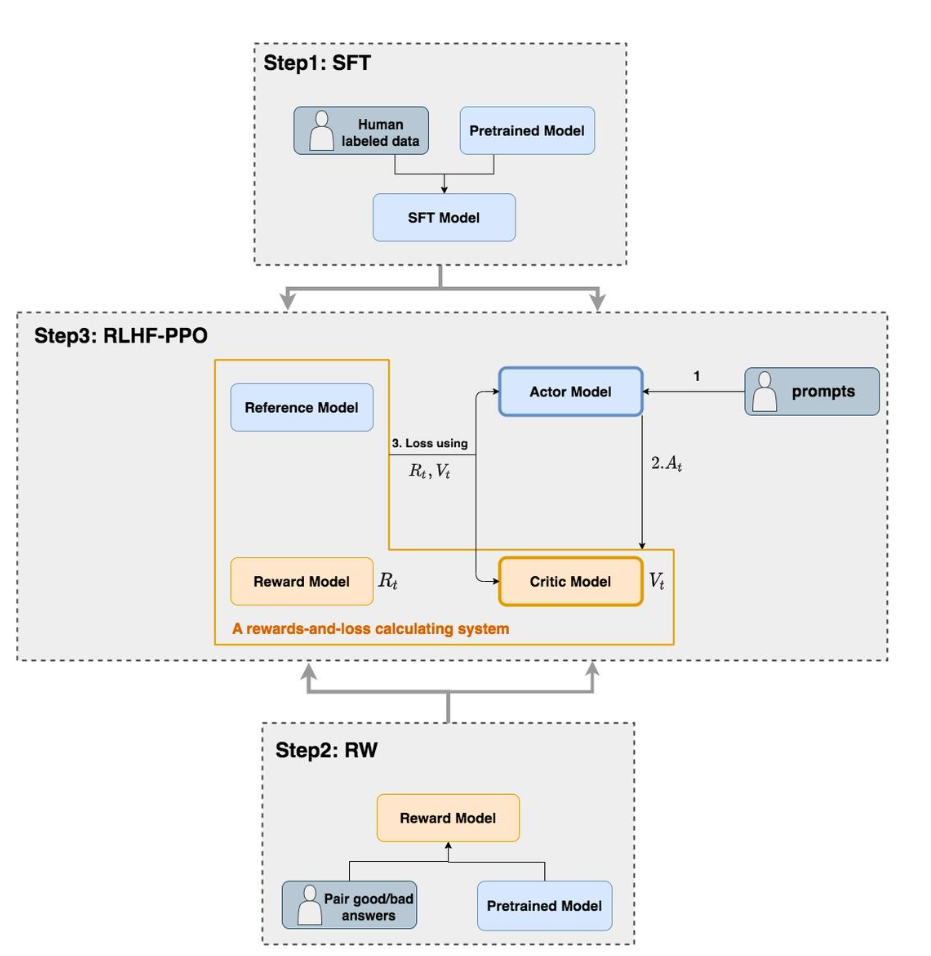
As shown in the diagram, during the RLHF-PPO stage, there are four main models:

Actor Model: The actor model is the target language model we want to train.
Critic Model: The critic model predicts the total return $V_t$ .
Reward Model: The reward model calculates the immediate reward $r_t$ .
Reference Model: The reference model is used to impose constraints on the language model during the RLHF phase to prevent it from deviating too much (i.e., it prevents the model from updating in an uncontrolled manner, which could lead to worse performance).

Details of the Models

Actor/Critic Models need to be trained during the RLHF phase (these models are highlighted with thick borders in the diagram). On the other hand, the Reward/Reference Models have their parameters frozen.
The Critic/Reward/Reference Models collectively form a “reward-loss” calculation system (a term I coined for better understanding), where we compute the loss by combining their results to update the Actor and Critic models.

Now, let’s break down each of these models in more detail:

Actor Model

As mentioned earlier, the Actor is the language model we aim to train. Typically, we initialize it using the model generated from the Supervised Fine-Tuning (SFT) stage.

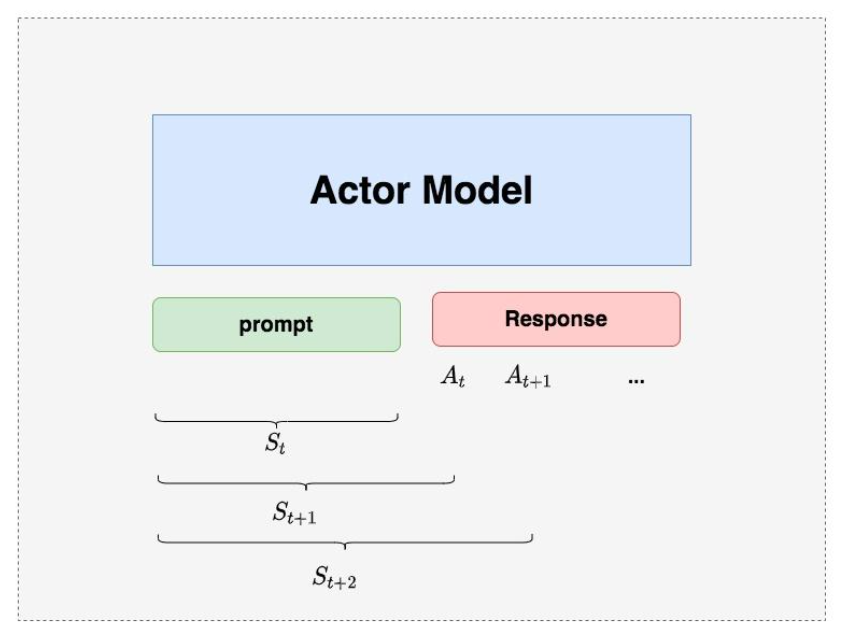
The goal is to train the Actor model to generate responses that align with human preferences. Our strategy is to first provide the Actor with a prompt (here we assume batch_size = 1, meaning a single prompt) and let it generate a corresponding response. Then, we feed the “prompt + response” into the “reward-loss” system to calculate the final loss, which will be used to update the Actor.

Reference Model

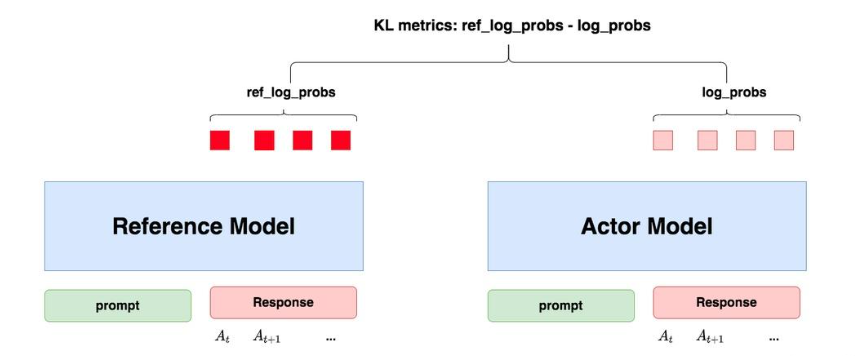
The Reference Model (abbreviated as Ref model) is also initialized using the model from the SFT stage, and its parameters are frozen during training. The primary function of the Ref model is to prevent the Actor model from “deviating.” But how exactly does it do this?

A more detailed explanation of “preventing the model from deviating” is that we want the Actor model to generate human-preference-aligned responses, while also ensuring that its output does not diverge too much from the SFT model. In short, we want the output distributions of both models to be as similar as possible. To measure the similarity of the output distributions, we use the KL divergence.

As shown in the diagram:

For the Actor model, we feed it a prompt, and it generates the corresponding response. Each token in the response has an associated log probability, which we denote as log_probs.
For the Ref model, we feed the prompt + response generated by the Actor model, and it also outputs the $log\_prob$ for each token, which we call $ref\_log\_probs$ .

The similarity between the output distributions of these two models can be measured by $ref\_log\_probs - log\_probs$ . This formula can be understood in two ways:

Intuitively: If $ref\_log\_probs$ is higher, it indicates that the Ref model is more confident in the output of the Actor model. In other words, the Ref model also believes that for some state $S_t$ , the probability of outputting some action $A_t$ is high $\left(P(A_t \mid S_t)\right)$ . In this case, we can say that the Actor model has not deviated from the Ref model.
From the perspective of KL divergence: In fact PPO has do some changes of KL divergence caculation. TL; DR: The Reference Model helps stabilize training by preventing large changes in the Actor’s behavior. We compare the log probabilities of the Actor and Reference Model’s outputs, which is a component used in PPO’s objective function. It’s important to note that this is not the full KL divergence, which is calculated over the entire probability distribution of possible outputs, not just the single chosen output.

In PPO, they often use a clipped surrogate objective, which includes this log probability difference, and sometimes a separate KL penalty term. The key is that the KL divergence is calculated over the entire distribution of actions, not just the action chosen by the actor.

To be more precise, the KL divergence between the actor’s policy and the reference policy at a given state s would be:

KL(\pi_\theta(\cdot|s) || \pi_{ref}(\cdot|s)) = \sum_{a \in A} \pi_\theta(a|s) \log \frac{\pi_\theta(a|s)}{\pi_{ref}(a|s)}

Where A is the set of all possible actions (tokens).

Now, we know how to use the Ref model and KL divergence to prevent the Actor from deviating too much. KL divergence will be used in the loss calculation, which will be explained in more detail later.

Critic Model

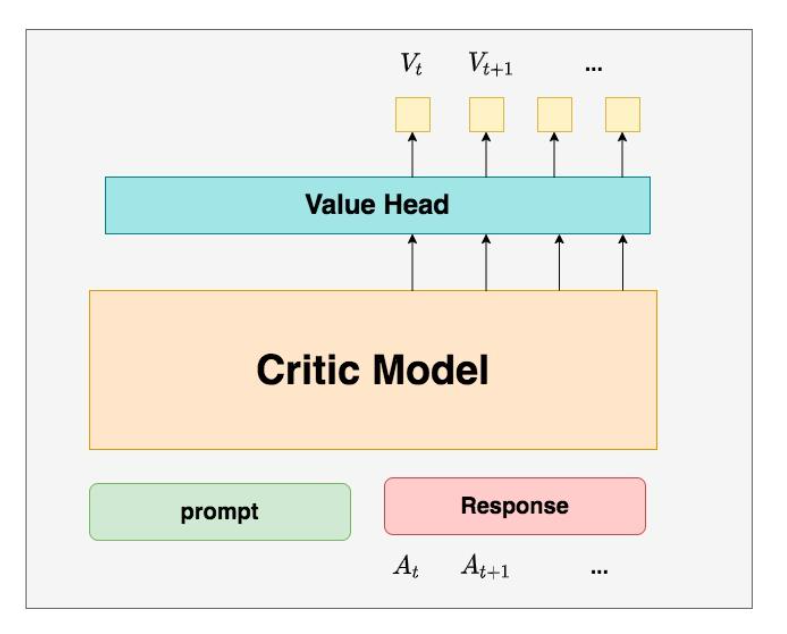
The Critic Model is used to predict the expected total return $V_t$ , and like the Actor model, it also requires parameter updates. In practice, the design and initialization of the Critic model vary, for example, it might share some parameters with the Actor model or be initialized from the Reward model trained during the RW stage. For consistency, we’ll assume here that it’s initialized from the Reward model of the RW stage.

You might wonder: I understand why we train the Actor model, but why do we need to train a separate Critic model to predict the return?

The reason is that when we discussed the total return $V_t$ (which includes both immediate and future rewards), we assumed an “omniscient perspective,” meaning that $V_t$ is the true, objective total return. However, when training the model, we no longer have this omniscient perspective. At time $t$ , we can’t access the true total return $V_t$ —instead, we train a model to predict it.

In summary, during RLHF, we need to train the model to generate content that aligns with human preferences (Actor), but we also need to improve the model’s ability to quantify human preferences (Critic). This is the purpose of the Critic model. The architecture of the Critic model is roughly as follows:

The Critic model is similar to the Actor model, but with an additional Value Head layer at the final stage. This layer is a simple linear layer that maps the raw output to a single value, representing the expected return $V_t$ .

Reward Model

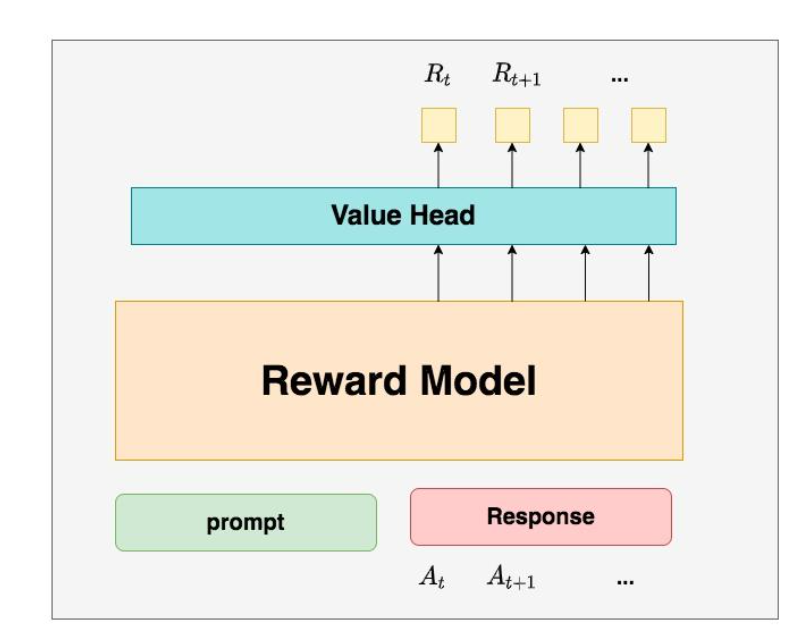
The Reward Model is used to calculate the immediate reward $r_t$ for generating token $a_t$ . It is the model trained during the RW stage, and its parameters are frozen during the RLHF phase.

You might ask: Why does the Critic model participate in training, but the Reward model, which is also related to the reward, has frozen parameters?

This is because the Reward model has an “omniscient perspective.” This omniscient perspective has two meanings:

The Reward model is trained with data related to “estimated rewards,” so during the RLHF phase, it can be used directly as a model that produces objective values.
The Reward model represents “immediate rewards,” meaning that since token $a_t$ has already been generated, the immediate reward can be computed right away.

You might also ask: I already have the Critic model predicting $V_t$ , which includes both “immediate” and “future” rewards, so why do I need the Reward model, which only represents the “immediate” reward?

To answer this question, let’s first review the value function:

$V_t = R_t + \gamma V_{t+1}$

This function tells us that the total reward at time $t$ can be represented by two results:

Result 1: The value predicted by the Critic model $V_t$
Result 2: The value predicted by the Reward model $R_t$ and the Critic model’s prediction for the next state $V_{t+1}$

Which of these two results is closer to the objective value from the “God’s eye perspective”? Of course, it is Result 2, because Result 1 is purely based on prediction, while $R_t$ in Result 2 is factual data.

We know that the Critic model is also involved in parameter updates. We can use the Mean Squared Error (MSE) to measure its loss, where the loss is the difference between the God’s eye perspective (the true reward) and the Critic model’s predicted value. However, since we do not know the objective reward from the “God’s eye perspective,” we can only approximate it using known factual data. Therefore, we use $R_t + \gamma V_{t+1}$ as an approximation. This is the reason why both $R_t$ and $V_t$ exist together.

The Reward and Critic models are quite similar.

Summary of these part

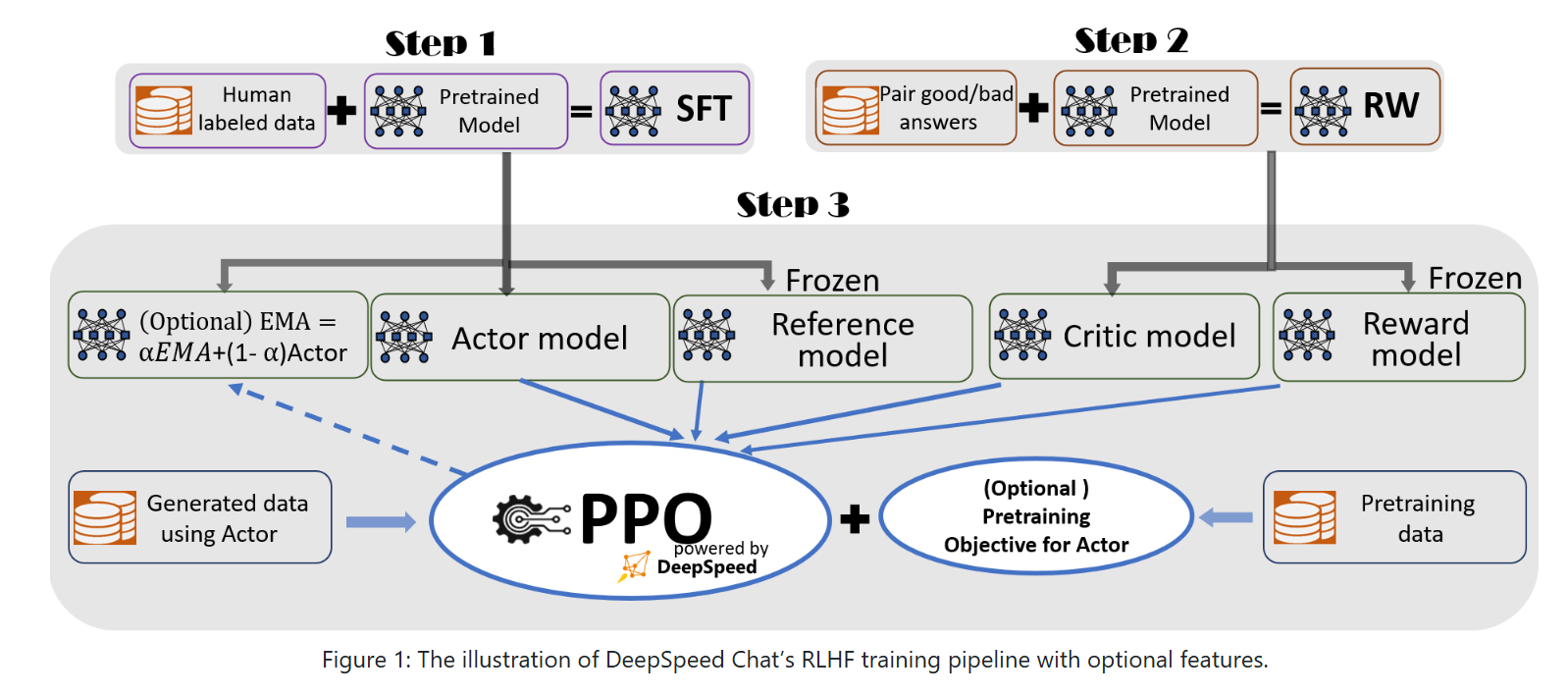
We can use this DeepSeppd Chat workflow to check our understading.

A breif summary:

Actor Model (The “Learner”):

Purpose: To generate responses that align with human preferences.
- Data: It is initialized using the SFT model (Supervised Fine-Tuned model) or other pre-trained models.
- Feedback: The Actor is updated using the reward-loss computation, which includes feedback from the Critic and Reward models.
- Frozen/Updated: Updated during RLHF.

Critic Model (The “Evaluator”):

Purpose: Predict the total future reward (both immediate and expected rewards) for the sequence generated by the Actor.
- Data: Typically initialized using the Reward Model from a previous phase (RW stage).
- Feedback: The Critic is trained based on the rewards the Actor generates, and it predicts the expected return for each response. Its output helps improve the Actor.
- Frozen/Updated: Updated during RLHF.

Reward Model (The “Immediate Reward Provider”):

Purpose: Provides the immediate reward for each token generated by the Actor.
Training:
- Data: The Reward Model is trained during the RW phase, where it learns to evaluate how well a generated token aligns with human preferences.
- Feedback: After training, the Reward Model gives immediate rewards to the Actor’s actions (tokens) during RLHF. This feedback is used to guide the Actor’s learning.
- Frozen/Updated: Frozen during RLHF (no updates).

Reference Model (The “Regulator”):

Purpose: Prevents the Actor from straying too far from the SFT model’s behavior and ensures the output distribution remains similar.
Training:
- Data: The Reference Model is also initialized using the SFT model and its parameters remain frozen during RLHF.
- Feedback: It compares the output of the Actor with its own output and provides feedback to regulate the Actor’s learning. Specifically, it uses KL divergence to measure how similar the distributions are between the Actor and the Reference.
- Frozen/Updated: Frozen during RLHF (no updates).

Key Points:

Actor: Updated with feedback from the Critic and Reward Models during RLHF. It learns to generate responses that are better aligned with human preferences.
Critic: Updated during RLHF to predict the total expected rewards (future returns) for each action the Actor takes.
Reward: Frozen after training during the RW phase and used to provide immediate feedback (rewards) for each token generated by the Actor.
Reference: Frozen during RLHF and used to help ensure the Actor’s output doesn’t diverge too much from the expected distribution of the SFT model, typically using KL divergence.

Go through some concepts

Let’s go through each comment in this source to identify which ones are correct and which ones are incorrect:

"Reward是对actor模型进行了某一个action之后的直接打分；而critic则是对这个actor模型的整体预估得分。"
- Correct.
  - Reward Model: Provides immediate feedback for each action taken by the Actor (i.e., a single token generated by the model).
  - Critic Model: Estimates the expected future total reward (both immediate and future rewards) for the sequence the Actor generates. The Critic assesses the long-term value of the Actor’s actions, not just the immediate reward.

"每次actor模型更新后，critic模型都要对这个新的actor模型重新打分，所以critic模型也要更新参数。"
- Incorrect.
  - Critic Model does not need to be updated after every update of the Actor model. In fact, in RLHF (Reinforcement Learning with Human Feedback), the Critic typically shares parameters with the Reward Model or is initialized from it, and only needs updates during training phases where its performance is evaluated against actual rewards.
  - The Critic’s role is to provide a value estimate that helps the Actor to improve its decision-making. While the Critic’s feedback helps guide the Actor, the Critic itself may not need to be updated as frequently as the Actor.

"critic模型对actor模型的整体预估得分，是根据reward模型的每一次实时打分来预估的。当critic模型的预估得分达到了一定的基准，就代表actor模型训练完成。"
- Partially Correct/Incorrect.
  - Correct: The Critic Model does estimate the overall future reward (the value of the entire action sequence) by considering the Reward Model’s immediate scores. The Critic aggregates the rewards over time, which are influenced by the Reward Model.
  - Incorrect: The Critic’s performance does not directly indicate when the Actor’s training is complete. The Critic serves to help the Actor learn by predicting the expected reward, but the Actor’s training completion is not directly tied to the Critic’s score reaching a specific threshold. In RLHF, the Actor continues to improve as long as there is a performance gap between the generated outputs and the desired outputs (aligned with human preferences).

"我感觉好像reward是一个句子生成结束之后打分，critic是token粒度的打分"
- Incorrect.
  - Reward Model provides feedback for each token (or action) generated by the Actor, not just at the end of the sentence. It’s more about giving immediate rewards for each action taken (each token generated).
  - Critic Model provides a value estimate over the entire sequence, not on a token-by-token basis. It predicts the total future reward based on the sequence of tokens produced by the Actor, incorporating both immediate and future rewards.

"reward模型，它是在第一阶段sft时，通过人工介入方式训练的一个能量化‘人类偏好’的模型，在PPO中的优势函数，要评估当前动作的好坏（即是否对齐人类偏好），自然就要用到这第一阶段训练到的reward模型来得到这个好坏值。也因此，这个reward网络在此阶段是冻结参数的。"
- Correct.
  - The Reward Model is trained in the SFT (Supervised Fine-Tuning) phase, where it quantifies human preferences by comparing different outputs. This model is then frozen during the RLHF phase, and the Actor uses it to evaluate its actions (tokens) based on how well they align with human preferences.

"最后，就是ref模型，从最基础的概念看，它是无关紧要的，但在rlhf里被引入，只是为了保证actor网络不被训偏（通过kl损失来约束）"
- Correct.
  - The Reference Model (Ref Model) is used in RLHF primarily to ensure that the Actor Model doesn’t diverge too far from the intended behavior (based on the SFT model). It does this by penalizing large differences in token generation distributions between the Actor and the Reference Model using KL Divergence.